文章

数组和字符串操作

发表于
作者 Giannis Chen
10 分钟阅读

数组和字符串操作（Array and String）

括号题

  • 括号题本质上是栈（Stack）的衍生，现在我们并不一定需要用实体的栈来模拟整个过程，仅用 $O(1)$ 的空间消耗，以栈的理念来实现，比如 921. Minimum Add to Make Parentheses Valid 这道题，通过两个变量计数（分别代表非法左括号和非法右括号的数目），来实现：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

    func minAddToMakeValid(s string) int {
	ans := 0
	stack := 0
	for i := 0; i < len(s); i++ {
		if s[i] == '(' {
			stack++
		} else {
			if stack > 0 {
				stack--
			} else {
				ans++
			}
		}
	}
	ans += stack
	return ans
}

区间操作

差分数组

  • 差分数组的元素都是一种差值：

    difference-array

  • 规则：

    \[DA[i] = \begin{cases} arr[i] & i=0 \\ arr[i]-arr[i-1] & i \neq 0 \\ \end{cases}\]

  • 例题：（1094. Car Pooling）

    • 车有有限的座位，每次运载都有起始地点和终点，是否能满足所有人的需要呢？我们想像一个时间轴，上面记录了每个时刻车上有多少人，就像 arr 中的一样，但是这样的更新是 $O(n)$ 复杂度的，当使用差分数组 DA 时，我只需要在 $DA[start]$ 上加上乘客数量， 在 $DA[end]$ 上减去来维持后序差分数组的正确性就行了。
    • 当然，最后别忘了一次遍历来进行统计。最后时间复杂度为 $O(n)$ ，空间复杂度为 $O(n)$ 。（当然题目中空间复杂度没那么高）

双指针

  • 以 15. 3Sum 为例，在数组中寻找三个元素（下标不同），让他们的和为零。暴力解法很显然需要 $O(n^3)$ 的时间复杂度，那么能不能优化成 $O(n^2)$ 呢？答案是可以的，需要用到的策略就是双指针。

    考虑以下的有序数组（无序先排一下序）：

    double-pointer

    当我们确定了 first 指向的数字时，我们就能确定剩下的两个数字之和希望 target 是多少，图中即 $nums[second]+nums[third] = 1$ ，按照之前的分析，暴力需要 $O(n^2)$ 的复杂度，但是面对有序数组，我们可以简化，不妨设 $nums[second]+nums[third]$ 为变量 tmp：

    1. 当前 tmp 等于 target ，是其中一个答案；
    2. 当前 tmp 小于 target ，左指针 second 向右移动，tmp 将变大；
    3. 当前 tmp 大于 target ，右指针 third 向左移动，tmp 将变小；

    由于数组有序，我们不需要回看已经遍历过的部分了，amazing！

  • 代码：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

    func threeSum(nums []int) [][]int {
	n := len(nums)
	ans := make([][]int, 0)
	sort.Ints(nums)
	for first := 0; first < n-2; first++ {
		if first > 0 && nums[first] == nums[first-1] {
			continue
		}
		target := -nums[first]
		for second, third := first+1, n-1; second < third; {
			if tmp := nums[second] + nums[third]; tmp == target {
				ans = append(ans, []int{nums[first], nums[second], nums[third]})
				second++
				for second < n && nums[second] == nums[second-1] {
					second++
				}
			} else if tmp < target {
				second++
			} else {
				third--
			}
		}
	}
	return ans
}

  • 其他经典问题：75. Sort Colors（Dutch national flag problem，荷兰国旗问题）

滑动窗口（sliding Windows）

  • 一个滑动窗口一般使用双指针来表示数组的开始和结束，分为两个步骤：
    1. 增长：当按题意寻找时，数组右指针会增长；
    2. 缩进：当右端按规则停住时，左侧按照某种规则判断是否能够缩进，如果能，数组左指针增长；
  • 例题 680. Valid Palindrome II ；

分治

  • 类似于归并排序的做法：

    190.001.jpeg

  • 例题 190. Reverse Bits

    1
2
3
4
5
6
7
8
9
10
11
12
13
14

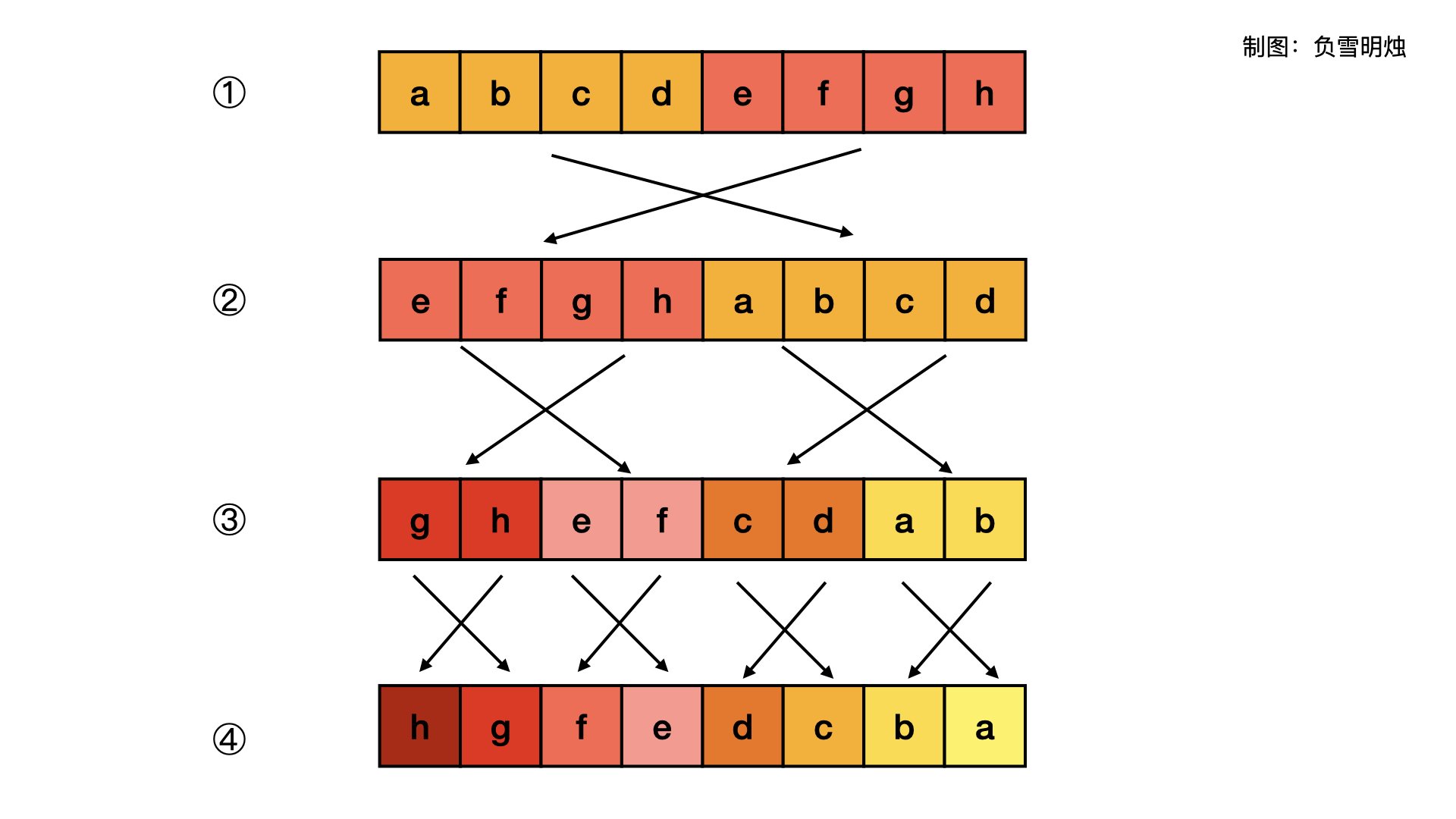
    const (
    m1 = 0x55555555 // 01010101010101010101010101010101
    m2 = 0x33333333 // 00110011001100110011001100110011
    m4 = 0x0f0f0f0f // 00001111000011110000111100001111
    m8 = 0x00ff00ff // 00000000111111110000000011111111
)
  
func reverseBits(n uint32) uint32 {
    n = n>>1&m1 | n&m1<<1
    n = n>>2&m2 | n&m2<<2
    n = n>>4&m4 | n&m4<<4
    n = n>>8&m8 | n&m8<<8
    return n>>16 | n<<16
}

回文字符串

形如 abcddcba 以及 abcdedcba 的字符串，即字符出现轴对称的情况，称为回文字符串。

如果要判断一个字符串是不是回文字符串，朴素的思想是：

1
2
3
4
5
6

for i := 0; i < len(s); i++ {
    if s[i] != s[len(s)-i-1] {
        return false
    }
    return true
}

但是扩展到要找所有的回文子串呢，如果还是朴素的方法，其复杂度过高了，时间复杂度为 $O(n^3)$ 。那么，我们引入一个新的方法，即中心扩展法：（例题：647. Palindromic Substrings，6236. Maximum Number of Non-overlapping Palindrome Substrings）

strings_huiwen_center

1
2
3
4
5
6
7
8
9
10
11
12
13

func countSubstrings(s string) int {
    n := len(s)
    ans := 0
    for i := 0; i < 2 * n - 1; i++ {
        l, r := i / 2, i / 2 + i % 2
        for l >= 0 && r < n && s[l] == s[r] {
            l--
            r++
            ans++
        }
    }
    return ans
}

字符串的子序列

判断一个字符串 word 是否是另一个字符串 s 的子序列，是比较简单的，最粗暴的是使用双指针遍历即可，其时间复杂度为 $O(n+m)$ 。但是，要是判断一组的字符串 words 呢，需要优化：

方法一：二分查找

  1. 对 s 做预处理，创建一个二维数组（哈希表），存放对应字母出现的位置下标 idx ：

    subsequence-match

  2. 每次匹配时，动用二分查找，找到恰好比 word 中上一个字母 idx 大的，如果没有，那么跳出。

方法二：分桶

（LeetCode 题解中较为巧妙的做法）

  1. 预处理阶段，words 中的各个 word 根据首字母分桶，每当遍历到 s 中的字母时，将对应的桶内字母去掉首字母重新进桶。
  2. 直到所有桶内都空了或者 s 遍历完了。

数组和字符串的例题

IDLeetCode 题号描述思路
1921. Minimum Add to Make Parentheses Valid统计将括号序列合法化最小括号添加的个数利用单个变量计数模拟栈操作
21249. Minimum Remove to Make Valid Parentheses删除最少的非法括号向前遍历 + 向后遍历
356. Merge Intervals区间合并排序 + 遍历
457. Insert Interval区间添加遍历 + 判断
51094. Car Pooling有限座位的车是否能运等车人差分数组
615. 3Sum三数之和为零双指针优化
775. Sort Colors三元素原地排序双指针
8680. Valid Palindrome II删除至多一个字符是否成回文串双指针
976. Minimum Window Substring满足要求的最小子串双指针滑动窗口
10190. Reverse Bits二进制倒置分治 或 遍历
11647. Palindromic Substrings回文子串的个数中心扩展法
126236. Maximum Number of Non-overlapping Palindrome Substrings不重叠回文字符串的最大数目中心扩展法 + DP
13792. Number of Matching Subsequences判断一系列字符串是否是某一字符串的子序列预处理 + 二分查找
题题题题
252. Meeting Rooms1272. Remove Interval435. Non-overlapping Intervals253. Meeting Rooms II
1229 Meeting Scheduler408 Valid Word Abbreviation1004 Max Consecutive Ones III209 Minimum Size Subarray Sum
1438 Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit Subsequence.792 Number of Matching Subsequences727. Minimum Window Subsequence940 Distinct Subsequences II

Subarray、substring （连续的）. From 1point 3acres bbs Rolling hash （Rabin-Karp） 1062. Longest Repeating Substring， 1044. Longest Duplicate Substring

LeetCode, LeetCode Tutorial
leetcode golang array string
本文由作者按照 CC BY 4.0 进行授权