文章

动态规划系列（0）综述

发表于
作者 Giannis Chen
32 分钟阅读

动态规划（Dynamic Programming）

  • 动态规划（Dynamic Programming）

  • 基本思路，对于一个能用动态规划解决的问题，一般采用如下思路解决：

    1. 将原问题划分为若干 阶段，每个阶段对应若干个子问题，提取这些子问题的特征（称之为 状态）；
    2. 寻找每一个状态的可能 决策，或者说是各状态间的相互转移方式（用数学的语言描述就是 状态转移方程）。
    3. 按顺序求解每一个阶段的问题。

  • 以 ID-1 为例，其状态转移方程为：$f(i+1)=\underset{0 \leq j \leq i}{max}f(j)$

    1
2
3
4
5
6
7
8
9
10
11
12
13
14

    func lengthOfLIS(nums []int) int {
	ans := 0
	dp := make([]int, len(nums))
	for i := 0; i < len(nums); i++ {
		dp[i] = 1
		for j := i - 1; j >= 0; j-- {
			if nums[i] > nums[j] {
				dp[i] = max(dp[i], dp[j]+1)
			}
		}
		ans = max(ans, dp[i])
	}
	return ans
}

记忆化搜索

  • 记忆化搜索一般和 DFS 结合，传统的 DFS 时间复杂度不太可控，尤其是一次搜索后其他节点可以重复访问，而非迷宫问题那样可以一次访问后不需要再次访问，即 $O(n*m)$ 。因此，记忆化搜索出现了，用空间换时间。

  • 如何写记忆化搜索：

    1. 把这道题的 dp 状态和方程写出来
    2. 根据它们写DFS 函数
    3. 添加记忆化数组

  • 例如在 ID-1 中，我们可以记录搜过的状态（即每个点）：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

    func lengthOfLIS(nums []int) int {
	mem := make([]int, len(nums))
	var dfs func(i int) int
	dfs = func(i int) (ret int) {
		if mem[i] != 0 {
			return mem[i]
		}
		ret++
		for j := 0; j < i; j++ {
			if nums[j] < nums[i] {
				ret = max(ret, dfs(j)+1)
			}
		}
		mem[i] = ret
		return
	}
  
	ans := 0
	for i := 0; i < len(nums); i++ {
		if mem[i] == 0 {
			ans = max(ans, dfs(i))
		}
	}
	return ans
}

背包DP

  • 背包问题是经典的 dp 题目，指一个容量有限的背包装最大价值的东西：

0-1背包

0-1背包 限制了物品有且只有一件，在背包最大质量为 $W$ 的情况下，能装物品价值最大，当然能有空位：

  • 首先考虑遍历到第 $i$ 个物品时，有两种状态，取或者不取，那么对于重量 $0 \leq j \leq W$ ，可以通过之前的状态获得，则有递推方程：

    \[f[i][j]=max(f[i-1][j],f[i-1][j-w_i]+v_i)\]

  • 显然这个方程只与 $i-1$ 的状态有关，就能通过滚动数组优化：

    \[f[j]=max(f[j],f[j-w_i]+v_i)\]

  • 但是，问题来了，当我按照 $j: w_i \to W$ 的顺序更新时，会影响到后面的状态，即物品选取了多次，这与题意违背，所以，采用反向遍历的方式 $j: W \to w_i$ 。

    务必牢记并理解这个转移方程，因为大部分背包问题的转移方程都是在此基础上推导出来的。

  • 代码：

    1
2
3
4
5

    for i := 0; i < len(w); i++ {
    for j := W; j >= w[i]; j-- {
        f[j] = max(f[j], f[j-w[i]]+v[i])
    }
}

  • 801. Minimum Swaps To Make Sequences Increasing 这一题作为开始还挺不错的，虽然这一题不知道为啥这么

完全背包

完全背包 不限制物品的件数，在背包最大质量为 $W$ 的情况下，能装物品价值最大，当然能有空位：

  • 模仿 0-1背包 问题，我们给出的递推方程：

    \[f[i][j]=\underset{0 \leq k \leq +\infty}{max} \{ f[i-1][j-k \times w_i]\}+k \times v_i\]

  • 然后优化这个方程，在替换为滚动数组的时候我们会发现，我们并不关心，顺序更新下（$j:0 \to W$），或者说可以利用之前更新的状态，而非担心被其污染；所以就有了以下方程：（跟 0-1背包 完全一样呢~）

    \[f[j]=max(f[j],f[j-w_i]+v_i) \qquad j:0 \to W\]

  • 代码：

    1
2
3
4
5

    for i := 0; i < len(w); i++ {
    for j := w[i]; j <= W; j++ {
        f[j] = max(f[j], f[j-w[i]]+v[i])
    }
}

多重背包

多重背包 限制物品的件数为 $k_i$，在背包最大质量为 $W$ 的情况下，能装物品价值最大，当然能有空位：

  • 同样模仿 0-1背包 ，我们可以朴素地写出递推方程：

    \[f[i][j]=\underset{0 \leq k \leq k_i}{max} \{f[i-1][j-k \times w_i]\}+k \times v_i\]

  • 上述方程的时间复杂度为 $O(W \cdot \sum_{i=1}^{n}k_i)$ 。因此我们从 $\sum{k_i}$ 处下手。因为我们考虑了大量相同的选择方案，比如 $k$ 件物品其实是一样的，因此不需要组合数的复杂度来选择，所以，可以使用二进制分组的方法进行优化。

  • 具体地说就是令 $A_{i,s}\; (s \in [0,\lfloor{log_2(k_i+1)}\rfloor-1])$ 分别表示由 $2^s$ 个单个物品“捆绑”而成的大物品。特殊地，若 $k_i+1$ 不是 $2$ 的整数次幂，则需要在最后添加一个由 $k_i-2^{\lfloor{log_2(k_i+1)}\rfloor-1}$ 个单个物品“捆绑”而成的大物品用于补足。时间复杂度降为：$O(W \cdot \sum_{i=1}^n log_2k_i)$

二维费用背包

有 $n$ 个任务需要完成，完成第 $i$ 个任务需要花费 $t_i$ 分钟，产生 $c_i$ 元的开支。

现在有 $T$ 分钟时间，$C$ 元钱来处理这些任务，求最多能完成多少任务。

  • 还是 0-1背包 的问题，我们直接从优化后的递推方程开始：

    \[f[i][j]=max(f[i][j],f[i-c[k]][j-t[k]]+1) \qquad \begin{cases} i:C \to c_i \\ j:T \to t_i \\ \end{cases}\]

分组背包

有 $n$ 件物品和一个大小为 $m$ 的背包，第 $i$ 个物品的价值为 $w_i$ ，体积为 $v_i$ 。同时，每个物品属于一个组，同组内最多只能选择一个物品，求背包能装载物品的最大总价值。

  • 这种题怎么想呢？其实是从「在所有物品中选择一件」变成了「从当前组中选择一件」，于是就对每一组进行一次 0-1 背包就可以了。

  • 代码：

    1
2
3
4
5
6
7
8
9

    for k:=0; k<len(package); k++ {
    for i:=w; i>=0; i-- {
        for j:=0; j<len(package[k]); j++ {
            if i>=package[k][j].w {
                dp[i]=max(dp[i],dp[i-package[i][j].w]+package[k][j].v)
            }
        }
    }
}

    这里要注意：一定不能搞错循环顺序，这样才能保证正确性。

区间DP

  • 区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。
  • 令状态 $f[i][j]$ 表示将下标位置 $i$ 到 $j$ 的所有元素合并能获得的价值的最大值，那么 $f[i][j]=max{f[i][k]+f[k+1][j]+cost}$ ， $cost$ 为将这两组元素合并起来的代价。
  • 区间 dp 有以下特点：
    • 合并：即将两个或多个部分进行整合，当然也可以反过来；
    • 特征：能将问题分解为能两两合并的形式；
    • 求解：对整个问题设最优值，枚举合并点，将问题分解为左右两个部分，最后合并两个部分的最优值得到原问题的最优值。

在一个环上有 $n$ 个数 $a_1,a_2,\dots,a_n$，进行 $n-1$ 次合并操作，每次操作将相邻的两堆合并成一堆，能获得新的一堆中的石子数量的和的得分，你需要最大化你的得分。

  • 首先考虑链上而不是环上的情况，状态转移方程很简单写出：

    \[f[i][j]=\underset{i\leq k \leq j-1}{max}\{f[i][k]+f[k+1][j]\}\]

  • 那么处理环上呢，我们可以复制整个链，变成 $2 \times n$ 个，其中第 $i$ 堆与第 $n+i$ 堆相同，用动态规划求解后，取 $f[1][n],f[2][n+2], \dots ,f[n-1][2n-2]$中的最优值，为最后的答案。

例题

  • 以ID-4 664. Strange Printer 为例，类似于 INSERT 模式切换成覆盖，求最小的写次数；不难发现，可以使用区间DP分割成子串计算，其转移方程：

    \[dp[i][j]= \begin{cases} dp[i][j-1] & s[i]=s[j] \\ \min_{i \leq k \leq j-1}dp[i][k]+dp[k+1][j] & s[i] \neq s[j] \\ \end{cases}\]

    感觉原理通了，这题不值得 hard 🤔

DAG有向无环图DP

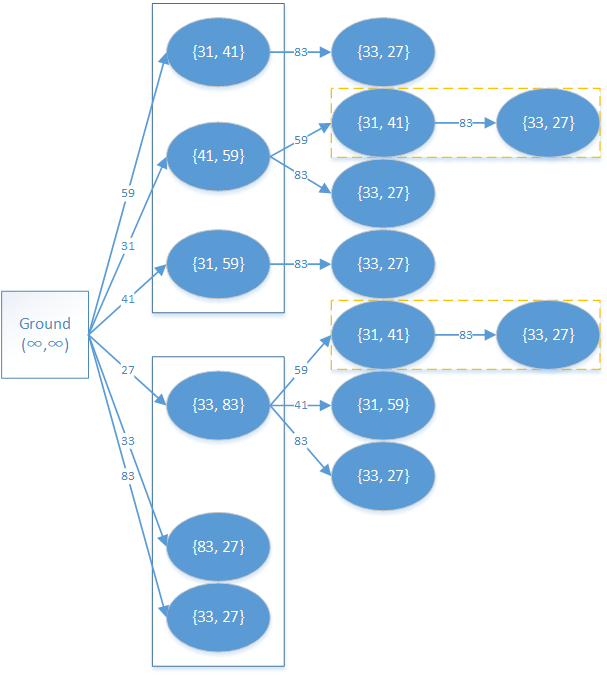
  1. 建立DAG，每一个节点表示一种姿态的方块 $(h,(a,b))$ ，其中 $(a.b)$ 是无序的，那么我们能建立一个DAG了。我们将以两种方块为例：$(31,41,59)$ 和 $(33,83,27)$

    img

    图中黄色虚线框表示的是重复计算部分，可以采用记忆化搜索的方法来避免重复计算。

  2. 下面我们开始考虑转移方程，设 $d(i,r)$ 表示第 $i$ 块砖块在最上面，且采用第 $r$ 种堆叠方式的最大高度。那么有如下的转移方程：

    \[d(i,r)=max\{d(j,r')+h\}\]

树形DP

  • 树形 DP，即在树上进行的 DP。由于树固有的递归性质，树形 DP 一般都是递归进行的。

某大学有 $n$ 个职员，编号为 $1 \sim N$ 。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 ，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

  1. 我们设 $f(i,0/1)$ 代表以 $i$ 为根的子树的最优解（第二维的值为 $0$ 代表 $i$ 不参加舞会的情况，$1$ 代表 $i$ 参加舞会的情况）。对于每个状态，都存在两种决策（其中下面的 $x$ 都是 $i$ 的儿子）：

    \[\begin{align} f[i][0] &= \sum \max\{f[x][1],f[x][0]\} \\ f[i][1] &= \sum f[x][0] + a_i \\ \end{align}\]

  2. 通过 DFS ，在返回上一层时更新当前节点的最优解。

例题

  1. 以 ID-3 LCP 64. 二叉树灯饰 为例，对于每个根节点 $i$，可见的几个状态分别为：

    • 不受任何祖先节点的影响，我们可以记为 $00$；

    • 受到开关2的影响，记为 $01$；

    • 受到开关3的影响，记为 $10$；

    • 受到开关2和开关3的影响，记为 $11$；

  2. 我们需要把所有灯都关上，所以最后的状态都应该是关灯；当前节点状态为 $1$ 时，我们可以使用一次开关和三次开关来改变状态；状态为 $0$ 时也类似，那么我们可以写转移方程和 DFS 了：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

    var dfs func(label int, node *TreeNode, state byte) int
dfs = func(label int, node *TreeNode, state byte) int {
    ...
    tmp := state
    // now off
    if switch_off {
        // do nothing
        ...
        // switch 1+2
        ...
        // switch 1+3
        ...
        // switch 2+3
        ...
    } else { // now on
        // switch 1
        ...
        // switch 2
        ...
        // switch 3
        ...
        // switch 1+2+3
        ...
    }
    total[label][tmp] = ret
    return total[label][tmp]
}
   
a := dfs(1, root, 0)
    \[f[u][state]=\min\{f[u*2][state_{next}]+f[u*2+1][state_{next}]+a_{switch}\}\]

    其中，$u$ 为当前节点编号，$state$ 为当前状态，$state_{next}$ 为下一个状态，这与开关选择有关，同时也要加上 $a_{switch}$ 这个状态转换消耗；😀（成功打卡第一道树形DP了属于是，可惜没在LCP之前学完~）

树上背包

现在有 $n$ 门课程，第 $i$ 门课程的学分为 $a_i$，每门课程有零门或一门先修课，有先修课的课程需要先学完其先修课，才能学习该课程。一位学生要学习 $m$ 门课程，求其能获得的最多学分数。

  1. 每门课最多只有一门先修课的特点，与有根树中一个点最多只有一个父亲结点的特点类似，因此可以想到根据这一性质建树。

  2. 如果所有课程组成了一个森林的结构，为了方便起见，我们可以新增一门 学分的课程（设这个课程的编号为 $-1$），作为所有无先修课课程的先修课，这样我们就将森林变成了一棵以 $-1$ 号课程为根的树。

  3. 接着模仿基础的树形DP和背包问题，提出递归过程，设 $f[u][i][j]$ 表示点 $u$ 为根的子树中，已经遍历了 $u$ 的前 $i$ 棵子树，选了 $j$ 门课程的最大学分，记点 $u$ 的儿子个数为 $s_u$，以 $x$ 为根的子树大小为 $size_x$，可以写出下面的状态转移方程：

    \[f[u][i][j]=\underset{v,k \leq j,k \leq size_v}{\max}\{f[u][i-1][j-k]+f[v][s_v][k]\}\]

  4. 参考代码：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

    #include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
int f[305][305], s[305], n, m;
vector<int> e[305];
   
int dfs(int u) {
  int p = 1;
  f[u][1] = s[u];
  for (auto v : e[u]) {
    int siz = dfs(v);
    // 注意下面两重循环的上界和下界
    // 只考虑已经合并过的子树，以及选的课程数超过 m+1 的状态没有意义
    for (int i = min(p, m + 1); i; i--)
      for (int j = 1; j <= siz && i + j <= m + 1; j++)
        f[u][i + j] = max(f[u][i + j], f[u][i] + f[v][j]);  // 转移方程
    p += siz;
  }
  return p;
}
   
int main() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) {
    int k;
    scanf("%d%d", &k, &s[i]);
    e[k].push_back(i);
  }
  dfs(0);
  printf("%d", f[0][m + 1]);
  return 0;
}

  5. （有空自己写个 Go 的…）

换根DP

  • 树形 DP 中的换根 DP 问题又被称为二次扫描，通常不会指定根结点，并且根结点的变化会对一些值，例如子结点深度和、点权和等产生影响。

  • 通常需要两次 DFS，第一次 DFS 预处理诸如深度，点权和之类的信息，在第二次 DFS 开始运行换根动态规划。

给定一个 $n$ 个点的树，请求出一个结点，使得以这个结点为根时，所有结点的深度之和最大。

  1. 不妨令 $u$ 为当前结点， 为当前结点的子结点。首先需要用 $s_i$ 来表示以 $i$ 为根的子树中的结点个数，并且有 $s_u=1+\sum s_v$ 。显然需要一次 DFS 来计算所有的 $s_i$ ，这次的 DFS 就是预处理，我们得到了以某个结点为根时其子树中的结点总数。

  2. 考虑状态转移，这里就是体现＂换根＂的地方了。令 $f_u$ 为以 $u$ 为根时，所有结点的深度之和。

  3. $f_v \leftarrow f_u$ 可以体现换根，即以 $u$ 为根转移到以 $v$ 为根。显然在换根的转移过程中，以 $u$ 为根或以 $v$ 为根会导致其子树中的结点的深度产生改变。具体表现为：

    • 所有在 $v$ 的子树上的结点深度都减少了 $1$，那么总深度和就减少了 $s_v$ ；

    • 所有不在 $v$ 的子树上的结点深度都增加了 $1$，那么总深度和就增加了 $n-s_v$ ；

  4. 根据这两个条件就可以推出状态转移方程 $f_v=f_u-s_v+n-s_v=f_u+n-2 \times s_v$ 。

  5. 于是在第二次 DFS 遍历整棵树并状态转移 $f_v=f_u+n-2 \times s_v$ ，那么就能求出以每个结点为根时的深度和了，最后只需要遍历一次所有根结点深度和就可以求出答案。

状压DP

  • 状压 DP 是动态规划的一种，通过将状态压缩为整数来达到优化转移的目的。

在 $N \times N$ 的棋盘里面放 $K$ 个国王（$1 \leq N \leq 9, 1 \leq K \leq N \times N$），使他们互不攻击，共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 $8$ 个格子。

  1. 设 $f[i][j][l]$ 表示前 $i$ 行，第 $i$ 行的状态为 $j$ ，且棋盘上已经放置 $l$ 个国王时的合法方案数。$x$ 为上一行某个状态，$sta(j)$ 表示状态 $j$里的国王个数，那么状态转移方程：

    \[f[i][j][l]=\sum f[i-1][x][l-sta(j)]\]

数位DP

  • 数位是指把一个数字按照个、十、百、千等等一位一位地拆开，关注它每一位上的数字。如果拆的是十进制数，那么每一位数字都是 $0 \sim 9$，其他进制可类比十进制。数位 DP用来解决这一类特定问题，这种问题比较好辨认，一般具有这几个特征：

    1. 要求统计满足一定条件的数的数量（即，最终目的为计数）；
    2. 这些条件经过转化后可以使用「数位」的思想去理解和判断；
    3. 输入会提供一个数字区间（有时也只提供上界）来作为统计的限制；
    4. 上界很大（比如 $10^{18}$），暴力枚举验证会超时。

  • 基本原理：

    • 考虑人类计数的方式，最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数，这样的过程中有许多重复的部分。例如，从 7000 数到 7999、从 8000 数到 8999、和从 9000 数到 9999 的过程非常相似，它们都是后三位从 000 变到 999，不一样的地方只有千位这一位，所以我们可以把这些过程归并起来，将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态，用递推或 DP 的方式进行状态转移。

    • 数位 DP 中通常会利用常规计数问题技巧，比如把一个区间内的答案拆成两部分相减（即

      \[ans_{[l,r]}=ans_{[0,r]}-ans_{[0,l-1]}\]

    • 那么有了通用答案数组，接下来就是统计答案。统计答案可以选择记忆化搜索，也可以选择循环迭代递推。为了不重不漏地统计所有不超过上限的答案，要从高到低枚举每一位，再考虑每一位都可以填哪些数字，最后利用通用答案数组统计答案。

  • 例题：（902. Numbers At Most N Given Digit Set，给定非零数字最多能组成多少个不超过 N 的数字）

    甚至可以不用显式 DP ，我们可以假装有个“0维” DP ，主要思想是由于不能超过 N ，那么选取正好小于 N 的数剩下部分就任选了；如果正好等于 N 的该数位，则看向下一个数位。找正好小于等于可以用二分查找简化，需要注意开头是可以为 0 的但是这次数字里不提供 0 ，由此带来的问题是，当 N 只有一位时该方法会多计算一个数值 0 ，需要额外去掉。

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

    func atMostNGivenDigitSet(digits []string, n int) int {
	ints := make([]int, 0)
	for i, digit := range digits {
		d, _ := strconv.Atoi(digit)
		if i == 0 || ints[len(ints)-1] != d {
			ints = append(ints, d)
		}
	}
  
	base := int(1e9)
	isFirst := true
  
	ans := 0
	for base > 0 {
		if n/base == 0 {
			base /= 10
			continue
		} else {
			d := (n / base) % 10
			i := sort.SearchInts(ints, d)
			if isFirst {
				ans += f(base/10, len(ints))
			}
			ans += i * f2(base/10, len(ints))
  
			if i == len(ints) || ints[i] != d {
				break
			} else {
				if base == 1 {
					ans++
				}
				isFirst = false
				base /= 10
			}
		}
	}
  
	if n < 10 {
		ans--
	}
	return ans
}
  
func f(base, num int) (res int) {
	item := 1
	if base == 0 {
		return 1
	}
	for base > 0 {
		item *= num
		res += item
		base /= 10
	}
	return
}
  
func f2(base, num int) int {
	item := 1
	if base == 0 {
		return 1
	}
	for base > 0 {
		item *= num
		base /= 10
	}
	return item
}

动态规划例题

IDLeetCode 题号描述思路
1300. Longest Increasing Subsequence最长递增子序列一维 DP，$f[i+1]=\underset{0 \leq j \leq i}{max}{f[j]}$
21143. Longest Common Subsequence最长公共子序列二维 DP，$f[i+1][j+1] = \begin{cases} f[i][j] & str1[i]=str2[j] \max(f[i+1][j],f[i][j+1]) & str1[i] \ne str2[j] \end{cases}$
3LCP 64. 二叉树灯饰二叉灯树开关问题树形DP，通过存储状态来减少搜索过程，即记忆化搜索
4664. Strange Printer覆盖打印，求最小打印次数区间DP，$dp[i][j] = \begin{cases} dp[i][j-1] & s[i]=s[j] \ \max_{i \leq k \leq j-1}(dp[i][j],dp[i][k]+dp[k+1][j]) & s[i] \ne s[j] \end{cases}$
5801. Minimum Swaps To Make Sequences Increasing两个数组对应位置进行交换DP，滚动数组
6LCP 69. Hello LeetCode!字典中取字符，代价最小DP + 状态压缩 + DP + DFS
7940. Distinct Subsequences II不同的子序列数$dp[i]=\sum_{j=’a’}^{‘z’}dp[j] \qquad ‘a’\leq i \leq ‘z’$
81235. Maximum Profit in Job Scheduling可以参加的工作的最多薪资以结束时间排序，结束时间相同时以经历时间最长为后，DP + 二分查找，注意二分查找的坑，因为结束时间有重复，需要找到最后一个…
92008. Maximum Earnings From Taxi赚钱最多的接乘客的方案同上一题的思路
101751. Maximum Number of Events That Can Be Attended II在限制数量的情况下可以参加的会议的最高价值同上题思路，不过增加一维来记录少于等于限制数量时，所能达到的最大价值
112054. Two Best Non-Overlapping Events在限制数量的情况下可以参加的会议的最高价值同上题，不过限制数量固定在 $2$ ，所以基本上 CV 就行
12902. Numbers At Most N Given Digit Set给定非零数字最多能组成多少个不超过 N 的数字标准数位 DP + 二分查找
13907. Sum of Subarray Minimums子数组的最小值之和DP + 单调栈
141140. Stone Game II石头游戏状态压缩搜索DFS
15174. Dungeon Game有掉血有加血的DP地牢一维DP优化二维，反向计算
16377. Combination Sum IV青蛙跳的加强版一维DP，但是二位循环
171039. Minimum Score Triangulation of Polygon多边形的三角剖分转换成区间DP
题题题题
354. Russian Doll EnvelopesLongest Substring Without Repeating Characters72. Edit Distance44. Wildcard Matching
10. Regular Expression Matching647. Palindromic Substrings5. Longest Palindromic Substring42. Trapping Rain Water
1423. Maximum Points You Can Obtain from CardsPalindrome problemsPrefix sum/max/minRange Sum Query - Immutable
304. Range Sum Query 2D - ImmutableWord Break 系列硬币零钱系列 Coin Change买股票系列 Best Time to Buy and Sell Stock
跳跃游戏系列 Jump games抢劫系列 House Robber石头游戏系列（Alice & Bob) Stone GameUnique Paths 系列
688 Knight Probability in Chessboard摘樱桃 Pick cherry174 Dungeon Game1277 Count Square Submatrices with All Ones
加油站问题 871. Minimum Number of Refueling Stops   
LeetCode, LeetCode Tutorial
leetcode golang dp
本文由作者按照 CC BY 4.0 进行授权