第341场周赛
第341场周赛
本场只有Q4有点意思,仅以此篇纪念我的LeetCode周赛AK。
Q4 最小化旅行的价格总和
现有一棵无向、无根的树,树中有 $n$ 个节点,按从 $0$ 到 $n - 1$ 编号。给你一个整数 $n$ 和一个长度为 $n - 1$ 的二维整数数组 $edges$ ,其中 $edges[i] = [a_i, b_i]$ 表示树中节点 $a_i$ 和 $b_i$ 之间存在一条边。
每个节点都关联一个价格。给你一个整数数组 $price$ ,其中 $price[i]$ 是第 $i$ 个节点的价格。
给定路径的 价格总和 是该路径上所有节点的价格之和。
另给你一个二维整数数组 $trips$ ,其中 $trips[i] = [start_i, end_i]$ 表示您从节点 $start_i$ 开始第 $i$ 次旅行,并通过任何你喜欢的路径前往节点 $end_i$ 。
在执行第一次旅行之前,你可以选择一些 非相邻节点 并将价格减半。
返回执行所有旅行的最小价格总和。
示例 1:
1
2
3
4
5
6
7
8
输入:n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出:23
解释:
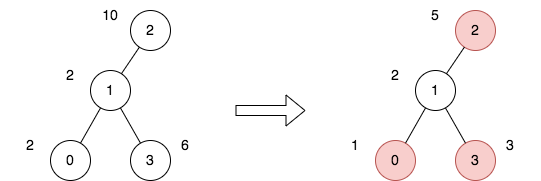
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树,第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行,选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行,选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行,选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明,23 是可以实现的最小答案。
示例 2:
1
2
3
4
5
6
输入:n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出:1
解释:
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树,第二个图表示选择节点 0 并使其价格减半后的树。
第 1 次旅行,选择路径 [0] 。路径的价格总和为 1 。
所有旅行的价格总和为 1 。可以证明,1 是可以实现的最小答案。
提示:
- $1 \le n \le 50$
edges.length == n - 1- $0 \le a_i,\, b_i \le n - 1$
edges表示一棵有效的树price.length == nprice[i]是一个偶数- $1 \le price[i] \le 1000$
- $1 \le trips.length \le 100$
- $0 \le start_i,\, end_i \le n - 1$
思路
看到非相邻节点的价格减半,自然而然想到了打家劫舍系列的337. 打家劫舍 III。只要通过一次DFS+树状DP判断即可,树状DP如何考虑呢?我们把他展平,对于每个节点,有两种情况,选或者不选。如果当前节点可以价格减半,那么其相邻节点都不能选;若不是,当前节点的相邻节点可选可不选,那我们有如下递推方程:(0表示不选当前节点current;1表示选择当前节点current作为价格减半)
那么$\cdots$这个部分应该填入点什么呢?我们发现,我们需要的是当前节点的访问数,为什么呢,访问过当前节点就会给总费用增加$price_i$或者$\frac{price_i}{2}$。所以,我们修改一下递推方程:
\[\begin{aligned} dp[cur][1] &= \frac{price_{cur}}{2} \times visits_{cur} + \sum_{son \neq father}{dp[son][0]} \\ dp[cur][0] &= price_{cur} \times visits_{cur} + \sum_{som \neq father}{\min(dp[son][0],dp[son][1])} \end{aligned}\]现在剩下唯一一个问题,如何统计当前节点访问过多少次呢?我们看一下题目,明显是要求A点到B点的最短路。如果我们在图中,第一反应是Floyd算法,复杂度是$O(n^3)$。但是我们在树里是可以简化的,怎么简化呢?最常见的是BFS,但是BFS不利于统计经过的节点,我们找到了终点B点,就要反向传播回起点A点。这句话正好对应了回溯+传递,那显然就是DFS了,我们只要判断是否搜到了终点,然后返回是终点,那么父节点自然也是树上的“关键路径”,因此visits也要累加,最终效果看看代码吧。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
func minimumTotalPrice(n int, edges [][]int, price []int, trips [][]int) int {
list := make([][]int, n)
for _, edge := range edges {
list[edge[0]] = append(list[edge[0]], edge[1])
list[edge[1]] = append(list[edge[1]], edge[0])
}
// count traverse nodes
vis := make([]int, n)
var dfs func(fa int, cur int, end int) bool
dfs = func(fa int, cur int, end int) (res bool) {
for _, next := range list[cur] {
if next == end {
vis[next]++
res = true
} else if next != fa {
res = dfs(cur, next, end)
}
if res {
vis[cur]++
break
}
}
return res
}
for _, trip := range trips {
start, end := trip[0], trip[1]
if start == end {
vis[start]++
} else {
dfs(-1, start, end)
}
}
// tree DP to find the node cut
var dfs2 func(fa int, cur int) (int, int)
dfs2 = func(fa int, cur int) (curNoCut int, curCut int) {
for _, next := range list[cur] {
if next != fa {
c1, c2 := dfs2(cur, next)
curNoCut += min(c1, c2)
curCut += c1
}
}
curCut += vis[cur] * (price[cur] / 2)
curNoCut += vis[cur] * price[cur]
return
}
c1, c2 := dfs2(-1, 0)
return min(c1, c2)
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
复杂度
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n)$