树链剖分

树链剖分之重链剖分

参考

• https://oi-wiki.org/graph/hld/

介绍

• 重链剖分能保证划分出的每条链上的节点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。可以用来：
  1. 修改 树上两点之间的路径上 所有点的值。
  2. 查询 树上两点之间的路径上 节点权值的 和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。
• 重链剖分可以将树上的任意一条路径划分成不超过$O(\log n)$条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点）。可以用来：
  1. $O(\log n)$（且常数较小）地求 LCA。

定义

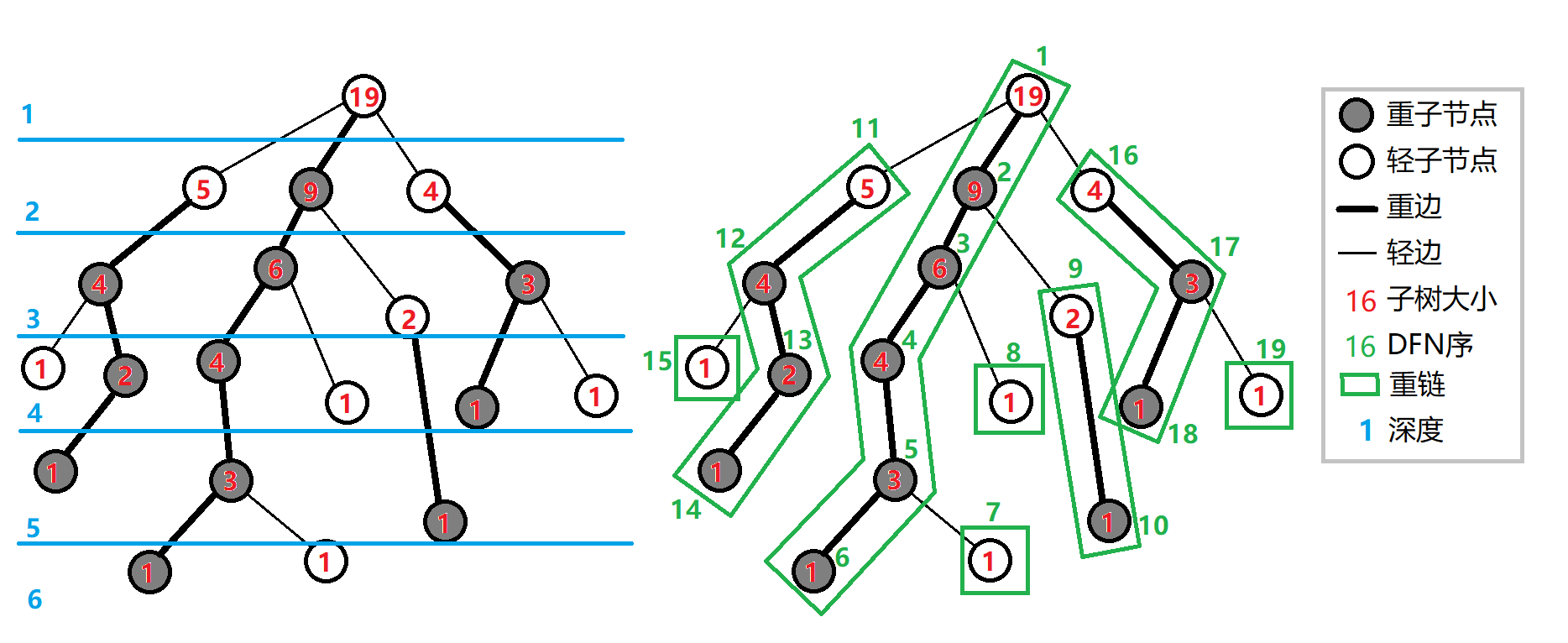
• 重子节点 —— 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一；如果没有子节点，就无重子节点；
• 轻子节点 —— 表示剩余的所有子结点；
• 重边 —— 从这个结点到重子节点的边；
• 轻边 —— 到其他轻子节点的边；
• 重链 —— 由若干条首尾衔接的重边构成；

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

实现

树剖的实现分两个 DFS 的过程。伪代码如下：

第一个 DFS 记录每个结点的父节点（father）、深度（deep）、子树大小（size）、重子节点（hson）。

int tree_build(u, dep) {
    u.hson = 0
	u.hson.size = 0
	u.deep = dep
	for each v in u.sons {
		u.size = u.size + tree_build(v, dep+1)
        v.father = u
            if v.size > u.hson.size {
                u.hson = v
            }
	}
    return u.size
}	

第二个 DFS 记录所在链的链顶（top，应初始化为结点本身）、重边优先遍历时的 DFS 序（dfn）、DFS 序对应的节点编号（rank）：

int tree_decomposition(u, top) {
    u.top = top
    idx += 1
    u.dfn = idx
    rank[idx] = u
    if u.hson {
        tree_decomposition(u.hson, top)
        for each v in u.sons {
            if v != u.hson {
                tree_decomposition(v, v)
            }
        }
    }
}

1. 第一遍：
   • $fa(x)$ 表示节点$x$在树上的父亲。
   • $dep(x)$表示节点$x$在树上的深度。
   • $siz(x)$表示节点$x$的子树的节点个数。
   • $son(x)$ 表示节点$x$的 重儿子。

2. 第二遍：

   • $top(x)$表示节点$x$所在 重链 的顶部节点（深度最小）。

   • $dfn(x)$ 表示节点$x$的 DFS 序，也是其在线段树中的编号。

   • $rnk(x)$表示 DFS 序所对应的节点编号，有$rnk(dfn(x))=x$。

应用

用树链剖分求树上两点路径权值和，伪代码如下：

int tree_path_sum(u, v) {
    idx = 0
    while u.top != v.top {
        if u.top.deep < v.top.deep {
            swap(u, v)
        }
        idx = idx + sum_range(u, u.top)
        u = u.top.father
    }
    idx = idx + sum_range(u, v)
    return idx
}